Carico critico euleriano
Si dice carico critico euleriano , per la teoria elastica della trave , quella forza di compressione il cui valore porta indefinitamente ad inflessione il solido snello su cui agisce, generando instabilità a carico di punta .
Caso in assenza di deformazioni taglianti Descrizione
Prendendo in considerazione un’asta realizzata con un materiale elastico lineare, soggetta ad uno sforzo normale centrato N e vincolata agli estremi con lo schema di semplice appoggio, la sollecitazione, nell’ipotesi di asta indeformata vale semplicemente σ = N / A ( sforzo normale ).
Supponendo che l’asta subisca uno sbandamento in modo che la sua linea d’asse (deformata) sia descritta dalla curva di equazione u ( x ) , la forza N produce anche un momento N u ( x ) , a cui si oppone il momento interno che, se si confonde la curvatura con la derivata seconda, vale E J u ''( x ) .
La condizione di equilibrio, per cui la configurazione deformata sia in equilibrio con la forza esterna, impone che la somma delle forze, interna ed esterna, sia nulla:
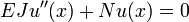
La cui soluzione, con le condizioni al contorno u (0) = u ( L ) = 0 è

dove

ed A e B sono costanti che dipendono dalle condizioni al contorno. Dalla condizione u (0) = A = 0 , segue che la prima delle due costanti è nulla. Considerando che u ''( L ) = B sin(α L ) = 0 , che ha due soluzioni possibili:
- se
 , deve risultare B = 0 . In questo caso la soluzione dell’equazione è
, deve risultare B = 0 . In questo caso la soluzione dell’equazione è 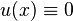 , ovvero la sola configurazione di equilibrio è quella indeformata.
, ovvero la sola configurazione di equilibrio è quella indeformata.
- se sen(α L ) = 0 allora la condizione al contorno è soddisfatta per qualunque
valore di B, pertanto esistono infinite configurazioni equilibrate (equilibrio indifferente).
La condizione s i n (α L ) = 0 implica che α L = n π , dove n indica un intero positivo. Ricordando la definizione di α , si ha che la precedente condizione è soddisfatta se

e questo si verifica per quei valori di N tali che

Il più piccolo dei valori di N n corrisponde al passaggio da una condizione di equilibrio stabile ad una instabile. Tale valore è quello per n = 1 , ed è detto il carico critico euleriano dell’asta compressa:

Indicando con N c r la forza critica, con J m i n il minimo fra i momenti d'inerzia della sezione trasversale, E il modulo di elasticità longitudinale, l 1 una dimensione da porre in relazione alla lunghezza effettiva l del solido e ai tipi di vincolo di cui questo è dotato, secondo la formula di Eulero, dove:
- l 1 = 2 l per trave incastrata ad un estremo e libera all'altro;
- l 1 = l per trave incerniera alle due estremità;
- l 1 = 0, 7 l per trave incastrata ad un estremo ed articolata all'altro;
- l 1 = 0, 5 l per trave incastrata ad ambedue gli estremi.
Dal carico critico ne deriva la tensione critica, cioè il valore della tensione raggiunto dall'asta quando N = N c r

con

La quantità λ viene chiamata "snellezza dell'asta" o semplicemente "snellezza".
Caso con deformazioni taglianti DescrizioneL'equazione della linea elastica è

Sostiuendo l'espressione di M e di T si ottiene

Da quest'ultima relazione si ottiene l'equazione differenziale del problema:

Per valori pari a  si ottiene l'equilibrio. La soluzione dell'equazione differenziale è del tipo
si ottiene l'equilibrio. La soluzione dell'equazione differenziale è del tipo
A e B sono costanti che dipendono dalle condizioni al contorno. Dalla condizione u (0) = A = 0 , segue che la prima delle due costanti è nulla. Considerando che u ( L ) = B s i n (α L ) = 0 , che ha due soluzioni possibili:
- se
 , deve risultare B = 0 . In questo caso la soluzione dell’equazione è
, deve risultare B = 0 . In questo caso la soluzione dell’equazione è 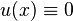 , ovvero la sola configurazione di equilibrio è quella indeformata.
, ovvero la sola configurazione di equilibrio è quella indeformata.
- se sen(α L ) = 0 allora la condizione al contorno è soddisfatta per qualunque valore di B, pertanto esistono infinite configurazioni equilibrate (equilibrio indifferente).
La condizione sen(α L ) = 0 implica che α L = n π , dove n indica un intero positivo. Ricordando la definizione di α , si ha che la precedente condizione è soddisfatta se

Il più piccolo dei valori di N n corrisponde al passaggio da una condizione di equilibrio stabile ad una instabile. Tale valore è quello per n = 1 , ed è detto il carico critico euleriano dell’asta compressa:
![N_{cr} = pi^2 frac{EJ_{min}}{l^2_1} frac{1}{left[ 1 +pi^2 left( frac{EJ_{min}}{l^2_1} frac{chi}{GA} right)right]}](http://upload.wikimedia.org/math/b/b/a/bbaed661f54b5d594483ba7b95b618d8.png) Tensione critica
Tensione critica Dal carico critico ne deriva la tensione critica, cioè il valore della tensione raggiunto dall'asta quando N = N c r
![sigma_{cr} = frac{N_{cr}}{A} = N_{cr} = pi^2 frac{EJ_{min}}{l^2_1 A} frac{1}{left[ 1 +pi^2 left( frac{EJ_{min}}{l^2_1} frac{chi}{GA} right)right]} = frac {pi^2 frac{E}{lambda^2}}{1 + frac{chi}{GA} A frac{E}{lambda^2}pi^2} = frac{pi^2 E}{lambda^2 + frac{chi}{GA} EA pi^2} = frac{pi^2 E}{lambda^2_{id}}](http://upload.wikimedia.org/math/6/b/a/6ba1b404ca6ce27da88c92ff50abc915.png) Voci correlate
Voci correlate 


 , deve risultare
, deve risultare 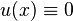 , ovvero la sola configurazione di equilibrio è quella indeformata.
, ovvero la sola configurazione di equilibrio è quella indeformata.